Python学习记录-矩形柱PM曲线分析

最近在翻看砼结构规范，觉得公式颇繁琐，于是想自己编程去计算下砼结构的截面承载能力。对于矩形柱子截面的PM曲线的生成与计算，其实有很简单的公式计算方法，可以采用EXCEL进行计算，刚好最近想玩下Python编程，于是决定采用Python进行编程计算。

计算案例介绍

案例矩形截面尺寸bxh = 500x600mm，截面配筋为单侧1901mm²，双侧对称配筋。钢筋中心到边缘的距离是35mm，混凝土等级为C30，钢筋采用HRB400，fy = 360MPa, fc = 14.3MPa（这里取砼结构规范的设计值，桥梁公预规取值比砼规范小）。在编程计算之前，采用程序XTRACT对截面的PM曲线进行分析，以验证自己编程计算的合理性。

图1 XTRACT截面PM计算结果（单位：N-m）

Python程序代码

采用Python编程计算，代码很简洁，几个语句就可以完成PM曲线计算，采用matplotlib进行曲线绘制，也是比较简单高效的。

计算代码如下：

import math
import matplotlib.pyplot as plt

## input section info
fc=14.3
b=500.0
h=600.0 
as1=35.0
h0=h-as1 
area=1900.7
fy=360.0
nstep=30
## input
pp=[]
mm=[]
a1=1.0 
beta1=0.8 
kxb=0.55 
##
n1=a1*fc*b*kxb*h0
nmax=a1*fc*b*h+2*area*fy
for i in range(nstep+1):
    nu=(i/nstep)*nmax 
    if nu<=nmax:
        if nu<=n1: 
            mu=-nu*nu/(2*a1*fc*b)+(nu*h)/2+fy*area*(h0-as1) 
        else:
            l1=(beta1-kxb)/(a1*fc*b*h0*(beta1-kxb)+fy*area) 
            l2=(kxb*fy*area)/(a1*fc*b*h0*(beta1-kxb)+fy*area) 
            k1=(l1*nu+l2)-0.5*(l1*nu+l2)*(l1*nu+l2) 
            kx1= l1*nu+l2 
            mu=a1*fc*b*h0*h0*(k1)-(h/2-as1)*nu+fy*area*(h0-as1) 
        pp.append(nu/1000)
        mm.append(mu/1e6)

ratio = area*2/(b*h)*100
plt.style.use('ggplot')
plt.plot(mm,pp,marker='o')
plt.xlabel('Moment')
plt.ylabel('Axial_Force')
plt.title("PM curve, Ratio = {0:.3f}".format(ratio))
plt.show()

with open('result.txt', 'w') as f:
    for i in range(nstep+1):
        f.write('{0:.2f}'.format(pp[i])+','+'{0:.5e}\n'.format(mm[i]))

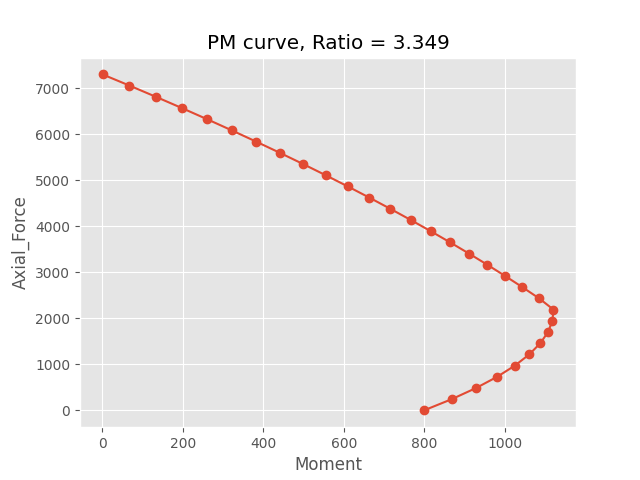图2 编程计算结果（单位：KN.m）

后记

如果要封装成一个小程序的话，可以用wxpython写界面，但是这么做需要使用者安装python的环境才能用。当然也有其他很不错的一些方法做成小程序发布，后续我会进行尝试再整理出来。