现浇箱梁横梁的计算方法讨论

横梁是现浇箱梁的一个重要构件，可以把主梁的荷载分配到各个支座上面，现行的规范没有给出相关的计算方法。在实际设计计算的过程中，针对单梁计算模型，计算主要原理就是把主梁的荷载等效施加在横梁上面，本文列举了一个横梁计算的例子，有一定的参考意义。

计算案例介绍

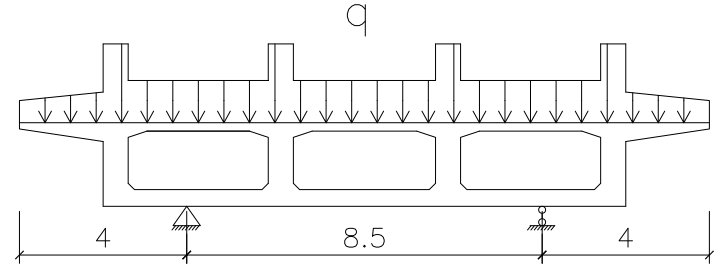
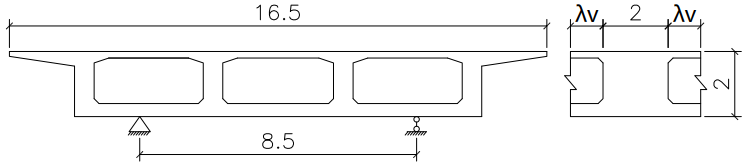
某现浇箱梁跨径：(30+37+37+30)米，中横梁宽度2米，梁高2米，箱梁支反力见下表：

表1 箱梁支反力

模型支座节点	恒载(kN)	活载最大(kN)	活载最小(kN)
1	4287	515	-71
21	14267	798	-90
41	14077	812	-103
61	14267	798	-90
81	4287	151	-71

图1 箱梁横断面图

活载取单车道的支反力，本文以41支座节点处的横梁计算为例。

横梁的计算加载模式

计算模式主要介绍了3种荷载传递到横梁上的方式，其中可变荷载效应均相同，所以下面的计算不考虑可变荷载效应，此外横梁截面均按矩形考虑，不考虑翼缘的贡献；但是空间有限元方法必须考虑翼缘的贡献，因为翼缘的应力还很大，否则计算出来的弯矩就是错误(偏小)的，此处翼缘的等效宽度采用顶底板形成的工形截面应力的变号点或者应力曲线凸凹点的宽度。

(一)等效重量法

等效重量法通过提高横梁的自重系数来等效箱梁对横梁本身的外荷载，加载图示见图2。设支反力为G_z，横梁自重为G_L，则自重提高系数β等于G_z/G_L。

图2 等效重量法加载模型

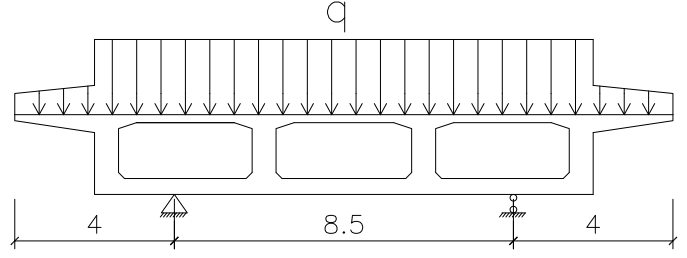
横梁投影面积为26.15m²，则GL=26.15×2×25=1307.5kN，本处横梁下支座支反力为G_z=14077kN，β=G_z/G_L=14077/1307.5=10.766。

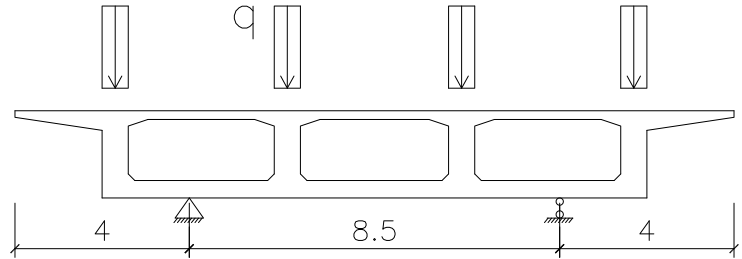
(二)等效剪力法

等效剪力法假设箱梁是通过剪力来对横梁进行加载的，等效剪力按接触面积分配，加载图示见图3，不考虑倒角影响，其接触面积Aj，剪应力τ等于(G_z-G_L)/A_j。

接触面积A_j为12.01m²，则τ=(14077-1307.5)/12.01=1063.2kN/m²。

图3 等效剪力法加载模型

(三)腹板剪力法

腹板剪力法假设箱梁的所有剪力是通过箱梁腹板传递到横梁上的，忽略上下顶板与横梁的作用，基本原理和梁格法相同。

图4 腹板剪力法加载模型

腹板宽度0.6米，则τ=(14077-1307.5)/(0.6×4×2) =2660.3kN/m²。

(四)空间有限元

采用ANSYS建立空间实体单元进行分析，采用空间四面体10节点SOLID92。支座位置采用线约束，因此在附近存在应力集中问题，压应力达到10.16Mpa，本处采用直径为一米的板式橡胶支座，在支座范围内进行削压，取支座左右0.5米位置的应力，压应力为2.24Mpa。

图5 上缘应力曲线

图6 下缘应力曲线表2 空间有限元结果

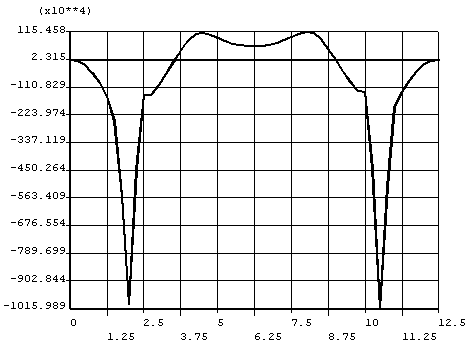
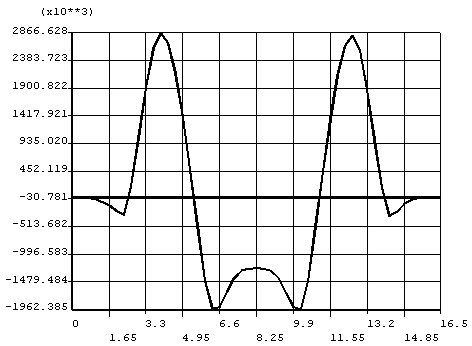
位置(m)	上缘应力(KP)	下缘应力(KP)	下缘宽度(m)	上缘宽度(m)	中性轴位置(m)	抗弯惯量(m4)	弯矩(kN.m)
4.00	2900	-2240	3.293	3.646	0.872	1.94	-4980
8.25	-1241	578	3.073	3.829	0.635	1.91	1738
12.50	2853	-2240	3.293	3.646	0.880	1.94	-4935

本表的中性轴位置计算是以中性轴位置应力为零进行计算得到的，本身截面的上下缘宽度为翼缘的等效宽度，用它来积分计算弯矩，但中性轴位置不能由它确定。

计算模式的比较

对于本例的箱梁横梁结构，上述四种模式的计算结果差别较大，其中等效重量法计算跨中弯矩最大，相应的支点负弯矩最小，计算结果与空间有限元分析结果偏差最大，而采用腹板剪力法计算是最接近实际情况的。各种模式计算结果比较见下表：

表3 计算模式的比较

编号	计算模式	支点位置(kN.m)	与有限元法比较	跨中位置(kN.m)	与有限元法比较
1	等效重量法	3068	小38%	6655	大283%
2	等效剪力法	4890	小2%	3790	大118%
3	腹板剪力法	5711	大15%	2347	大37%
4	空间有限元	4980		1738

实际上在横梁计算的时候应该具体情况具体分析，比如对于支座在腹板位置的情况，本文没有进行分析，但是此时腹板剪力法就偏不保守，采用等效剪力法或者等效重量法会更加合理。另外对于预应力结构，计算结果偏保守会使横梁上缘产生拉应力，因此对于计算模式的选择应慎重。