合理成桥索力优化原理及优化模型

由于部分斜拉桥一般跨径较小，索长较小，因而可忽略拉索垂度效应的影响，采用基于线性叠加原理的影响矩阵法进行成桥索力计算。一般情况下，部分斜拉桥的主梁及索塔截面积均较大，分析时可忽略因拉索索力变化引起的结构轴力、剪力应变能，但应对主梁的轴力和弯矩范围进行限制。

索力影响矩阵

取斜拉索的初张拉力为变量，以各斜拉索的单位初张力分别作用于无应力状态的结构，得到对主梁各单元杆端力的影响值而组成影响矩阵。设：

｛X｝—为斜拉索初张力列阵；

｛P｝—为斜拉索索力列阵；

｛M｝—为结构各单元杆端弯矩列阵｛M₁^L M₁^R M₂^L M₂^R…M_m^L M_m｝^T，M_i^L M_i^R分别为第i号单元左右端弯矩；

｛N｝—为结构各单元杆端轴力列阵｛N₁^L N₁^R N₂^L N₂^R…N_m^L N_m｝^T，N_i^L N_i^R分别为第i号单元左右端轴力；

​ 则｛P｝=｛P_D｝+[A_P]{X} (1)

​ ｛M｝=｛M_D｝+[A_M]{X} (2)

​ ｛N｝=｛N_D｝+[A_N]{X} (3)

其中，｛P_D｝、｛M_D｝、｛N_D｝—分别为恒载作用下的索力列阵和i结构各单元杆端的弯矩、轴力列阵；｛M_D｝=｛M_D1^L M_D1^R M_D2^L M_D2^R…M_Dm^L M_Dm｝^T，M_Di^L M_Di^R分别为第i号单元左右端恒载弯矩；｛N_D｝=｛N_D1^L N_D1^R N_D2^L N_D2^R…N_Dm^L N_Dm｝^T，N_Di^L N_Di分D别为第i号单元左右端恒载轴力；[A_P]、[A_M]、[A_N]—分别为索力影响矩阵和各单元杆端弯矩、轴力影响矩阵，即单位初张力作用下的索力和各单元杆端弯矩、轴力。

优化目标函数

通常情况下采用有约束的最小能量法对结构进行优化，可选结构的势能（弯曲和拉压应变能）U作为优化目标函数。

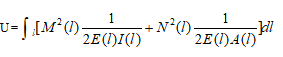
假定主梁各单元均为等截面，单元的弹性模量不变，则上式可简化为：

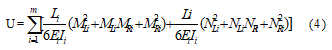
式中，M_i^L M_i^R分别为第i号单元左右端弯矩；N_i^L N_i^R分别为第i号单元左右端轴力；Ei、Ii、Ai、Li—分别为第i号主梁单元的弹性模量、截面惯性矩、截面积和单元长度；m为结构的单元数。

将式（2）、（3）带入式（4）并用矩阵形式表示为：

U={X}^T[G]{X}+2{F}^T{X}+D (5)

式（5）中:G=[A_M]^T[B][A_M]+[A_N]^T[C][A_N];F=[M_D]^T[B][A_M]+[N_D]^T[C][A_N]；

D=[M_D]^T[B][M_D]+[N_D]^T[C][N_D]。

其中[B]、[C]分别为单元柔度对单元弯矩、单元轴力的加权系数矩阵：

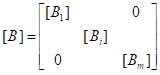
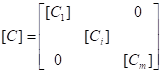
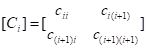
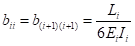
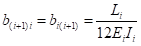
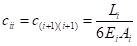
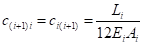
无约束索力优化的线性方程解

要使索力调整后结构应变能最小，令：

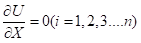
式中，n为调整索数。

将式（4）代入式（5）并写成矩阵形式：

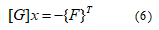
至此，索力优化问题转化为求解（6）式的一阶线性方程的问题。

优化约束条件

（1）索力约束条件

斜拉索的索力在成桥状态及运营过程中，考虑到强度和疲劳问题，应约束索力的上下极限值。另外初张索力及正常使用过程中的索力应为大于0的拉力，以确保斜拉索的有效性。因此，索力约束条件为：

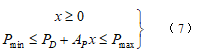
其中，P_max、P_min为指定索力上、下限值。

（2）位移约束条件

斜拉桥的梁部线形及索塔的水平位移由于在施工过程中可采用预设预拱度的方法以达到理想状态，但由于斜拉桥各部分的计算变形量能直观反映全桥的设计是否合理，所以仍然是设计者所关心的。位移约束可表示为：

D_min ≤D_D+A_Dx≤D_max（8)

其中，A_D为节点位移矩阵；D_D为结构自重作用下的节点位移列阵；D_max、D_min为指定位移上、下极限值。

（3）主梁内力约束条件

在成桥状态下，主梁的恒载弯矩要控制在”可行域”范围内。弯矩约束可表示为：

M_min ≤M_D+A_Mx≤M_max （9）

其中，M_max、M_min为指定弯矩上、下极限值。

拉索索力优化模型

综上所述，拉索索力优化的数学模型可归纳为：

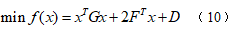
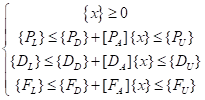
可见，以上索力优化数学模型为二次线性规划问题，本文借助MATLAB优化工具箱对优化模型进行求解。